前にかいたこれですけど、普通の人はMatlab / Ocatave / Scilabの様なソフトウェアはPCに入っていないから、補足としてブラウザのJavaScriptで動く物を用意しました。
電子ボリュームのカーブに迷ったときに、このページを活用ください。
このページは Controlling Volume—log pots を参考にしました。 あわせて参照ください。
減衰器のモデル
A群(対数型)抵抗変化特性を表す記号 - “JIS C5260-1:2014”
よりオーディオ用可変抵抗器の抵抗変化特性 15Aを参考にしました。1
対数型抵抗変化特性とはいえ、対数なのは人の感覚の方なので 人が感覚的に直線変化するように感じる変化特性は対数グラフ紙に書かれた直線のような指数関数だと思いますよ。
モデルの関数
位置 $p~(0 \leqq p \leqq 1)$
$p=0$ で減衰量最大および $p=1$ で減衰量最小出力電圧/入力電圧比 $\left( \frac{Vout}{Vin} \right) = y$
底が $\mathrm e$
である指数関数を
$$ \Large y= \mathrm e ^{a(p-1)} \tag1 $$
とおく。 その両辺の対数をとって
$$ \log y = a(p - 1) \\[1em] a = \frac{\log y}{p - 1} \tag 2 $$
題意より $p=0.5, ~y=0.1$ を $ (2) $ 式に代入して
$$ a = \frac{\log~ 0.1}{0.5 - 1} \approx 4.6052 \tag 3 $$
よって 50%(中央位置)で10%の点を通過する指数関数は $ (1),~(3) $ 式より
$$ y = \mathrm e^{a(p-1)} \approx \mathrm e^{4.6052~(p-1)} $$
このグラフでわかるとおり位置0%の時に0%にならないので,電子ボリュームにこのモデルは使いにくい。
位置0%(最も絞った)時には
$ (1) $ 式より
$$ \frac{Vout}{Vin} = y = \large {\mathrm e ^{\frac{\log 0.1}{0.5-1}(0.0-1)} = 0.01} $$
デシベルの定義より
$$ Gain = 20 \cdot \log_{10} {\frac{Vout}{Vin}} $$
よって
$$ Gain = 20 \cdot \log _{10} ~0.01 = -40 ~ \mathrm{dB} $$
つまり、このまま使えば位置0%で -40dB しか絞れないボリュームになるのであった。
体験してみるとわかりますが 入出力比 0.01 = 1% = ゲイン -40dB は普通に音がきこえますからね。
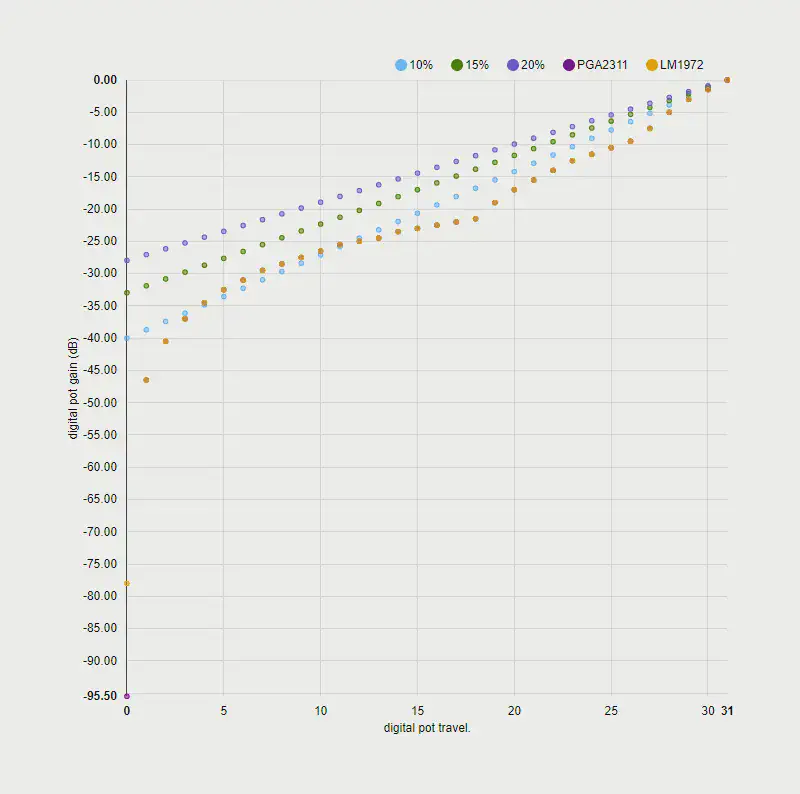
電子ボリュームICの設定値-減衰量
電子ボリュームIC(LM1972, PGA2311)のデーターシートより設定値-減衰量を読み取ってここに用意しました。
LM1972は減衰のみですが、PGA2311は増幅も出来ることがこのグラフからわかります。
ですが今回は増幅機能は使わずに、減衰器にしか使いません。23
https://codesandbox.io/s/poticcurve-79lit
直線を曲げた減衰曲線
電子ボリュームには
- 位置0%の時に0%になる直線
- 位置100%の時に100%になる直線
- 45度直線
を組み合わせた減衰曲線を使うことにします。