「巨人版ヘッドホンアンプ」を使うために必要にせまられて+15Vから-15Vを作る反転コンバータを設計してたところにバーグラフネオン管 in-9
が到着した。
ということで
電源回路トポロジー 今回設計する電源の回路トポロジーは昇圧コンバータになります。
出力電力は 150V × 12mA(in-9の定格最大電流) × 14(本) = 25.2W以上, ヘッドホンアンプ用に12W と若干の余裕を見込んで39Wとする。
諸元 最低入力電圧 V I N ( m i n ) : 14 V V_{IN \mathrm{(min)}} : 14 \mathrm{V} V I N ( min ) : 14 V 標準入力電圧 V I N : 15 V V_{IN} : 15 \mathrm{V} V I N : 15 V 最大入力電圧 V I N ( m a x ) : 15 V V_{IN \mathrm{(max)}} : 15 \mathrm{V} V I N ( max ) : 15 V 出力電圧 V O U T : 150 V V_ \mathrm{OUT} : 150 \mathrm{V} V OUT : 150 V ダイオードの順方向電圧 V F : 1.5 V V_F : 1.5 \mathrm{V} V F : 1.5 V 最大出力電力 P O U T ( m a x ) : 39 W P_{OUT \mathrm{(max)}}: 39 \mathrm{W} P O U T ( max ) : 39 W 効率 η : 70 \eta : 70 η : 70 スイッチング周波数 f s w : 116 k H z f_{sw} : 116 \mathrm{kHz} f s w : 116 kHz インダクタのインダクタンス値 資料
最大出力電流(ヘッドホンアンプ用も含んで) I O U T ( m a x ) = P O U T ( m a x ) V O U T = 39 150 = 260 m A
\begin{aligned}
I_{OUT \mathrm{(max)}} &= \frac{P_{OUT \mathrm{(max)}}}{V_{OUT}} \\
&= \frac{39}{150} \\
&= 260~\mathrm{mA}
\end{aligned}
I O U T ( max ) = V O U T P O U T ( max ) = 150 39 = 260 mA
通流率(Duty cycle) D = 1 − V I N ( m i n ) × η V O U T = 1 − 14 × 0.70 150 = 0.93
\begin{aligned}
D &= 1 - \frac{V_{IN \mathrm{(min)}} \times \eta}{V_{OUT}} \\
&= 1 - \frac{14 \times 0.70}{150} \\
&= 0.93
\end{aligned}
D = 1 − V O U T V I N ( min ) × η = 1 − 150 14 × 0.70 = 0.93
インダクタに流れるリプル電流 Δ I L = ( 0.2 t o 0.4 ) × I O U T ( m a x ) × V O U T V I N = 0.2 × 260 × 1 0 − 3 × 150 15 = 0.52 A
\begin{aligned}
\Delta I_L &= (0.2 ~~ to ~~ 0.4) \times I_{OUT \mathrm{(max)}} \times \frac{V_{OUT}}{V_{IN}} \\
&= 0.2 \times 260 \times 10^{-3} \times \frac{150}{15} \\
&= 0.52~\mathrm{A}
\end{aligned}
Δ I L = ( 0.2 t o 0.4 ) × I O U T ( max ) × V I N V O U T = 0.2 × 260 × 1 0 − 3 × 15 150 = 0.52 A
インダクタのインダクタンス値 L = V I N × ( V O U T − V I N ) Δ I L × f s w × V O U T = 15 × ( 150 − 15 ) 0.52 × 114 × 1 0 3 × 150 = 228 μ H
\begin{aligned}
L &= \frac{V_{IN} \times (V_{OUT} - V_{IN})} {\Delta I_L \times f_{sw} \times V_{OUT}} \\
&= \frac{15 \times (150 - 15)}{ 0.52 \times 114 \times 10^3 \times 150} \\
&= 228~\mathrm{\mu H}
\end{aligned}
L = Δ I L × f s w × V O U T V I N × ( V O U T − V I N ) = 0.52 × 114 × 1 0 3 × 150 15 × ( 150 − 15 ) = 228 μ H
なんか違和感があるので
通流率 α は(資料α = T o n ÷ T
\alpha = T_{on} \div T
α = T o n ÷ T
昇圧チョッパの通流率(Duty)は(おなじく資料V o u t = V i n ÷ ( 1 − α )
V_{out} = V_{in} \div ({1-\alpha})
V o u t = V in ÷ ( 1 − α )
両辺をVinで割ってV o u t V i n = 1 1 − α
\frac{V_{out}}{V_{in}} = \frac{1}{1-\alpha}
V in V o u t = 1 − α 1
両辺を-1乗して( V o u t V i n ) − 1 = ( 1 1 − α ) − 1
\left( \frac{V_{out}}{V_{in}} \right) ^ {-1} = \left( \frac{1}{1-\alpha} \right) ^ {-1}
( V in V o u t ) − 1 = ( 1 − α 1 ) − 1
両辺を-1乗するというのは, つまりこのことで
1 ( V o u t V i n ) = 1 ( 1 1 − α )
\frac{1}{\left( \frac{V_{out}}{V_{in}} \right)} = \frac{1}{\left( \frac{1}{1-\alpha} \right)}
( V in V o u t ) 1 = ( 1 − α 1 ) 1
1 ÷ ( V o u t V i n ) = 1 ÷ ( 1 1 − α )
1 \div {\left( \frac{V_{out}}{V_{in}} \right)} = 1 \div {\left( \frac{1}{1-\alpha} \right)}
1 ÷ ( V in V o u t ) = 1 ÷ ( 1 − α 1 )
分数の割り算は分母分子を入れ替ると掛け算になるので
1 × ( V i n V o u t ) = 1 × ( 1 − α 1 )
1 \times {\left( \frac{V_{in}}{V_{out}} \right)} = 1 \times {\left( \frac{1-\alpha}{1} \right)}
1 × ( V o u t V in ) = 1 × ( 1 1 − α )
1は乗法単位元だから, 1をかける計算はそれを取り除いた式と同じでV i n V o u t = 1 − α
\frac{V_{in}}{V_{out}} = 1-\alpha
V o u t V in = 1 − α
両辺にαをたしてV i n V o u t + α = 1
\frac{V_{in}}{V_{out}} + \alpha = 1
V o u t V in + α = 1
両辺から V i n V o u t \frac{V_{in}}{V_{out}} V o u t V in α = 1 − V i n V o u t
\alpha = 1 - \frac{V_{in}}{V_{out}}
α = 1 − V o u t V in
代入するとこう。α = 1 − 15 150 = 0.9
\alpha = 1 - \frac{15}{150} = 0.9
α = 1 − 150 15 = 0.9
ということで, 別の資料
*** 入力電流の平均値 I L ( D C M A X ) I_{L \mathrm{(DC~MAX)}} I L ( DC MAX ) I L ( D C M A X ) = V O U T × I O U T ( M A X ) V I N ( T Y P ) × η = P O U T ( m a x ) V I N ( T Y P ) × η = 39 15 × 0.70 = 3.7 A
\begin{aligned}
I_{L \mathrm{(DC~MAX)}} &= \frac{V_{OUT} \times I_{OUT \mathrm{(MAX)}}} {V_{IN \mathrm{(TYP)}} \times \eta} \\
&= \frac{P_{OUT \mathrm{(max)}}} {V_{IN \mathrm{(TYP)}} \times \eta} \\
&= \frac{39}{15 \times 0.70} \\
&= 3.7~\mathrm{A}
\end{aligned}
I L ( DC MAX ) = V I N ( TYP ) × η V O U T × I O U T ( MAX ) = V I N ( TYP ) × η P O U T ( max ) = 15 × 0.70 39 = 3.7 A
インダクタに流れるリプル電流 Δ I L ( P − P ) = ( 20 % ∼ 40 % ) × I L ( D C M A X ) = 0.2 × 3.7 = 0.74 A
\begin{aligned}
\Delta I_{L \mathrm{(P-P)}} &= (20 \% \sim 40 \%) \times I_{L \mathrm{(DC~MAX)}} \\
&= 0.2 \times 3.7 \\
&= 0.74~\mathrm{A}
\end{aligned}
Δ I L ( P − P ) = ( 20% ∼ 40% ) × I L ( DC MAX ) = 0.2 × 3.7 = 0.74 A
インダクタのインダクタンス値 L = V I N × ( V O U T + V D − V I N ) Δ I L ( P − P ) × f s w × ( V O U T + V D ) = 15 × ( 150 + 1.5 − 15 ) 0.74 × 114 × 1 0 3 × ( 150 + 1.5 ) = 160 μ H
\begin{aligned}
L &= \frac{V_{IN} \times (V_{OUT} + V_D - V_{IN})} {\Delta I_{L \mathrm{(P-P)}} \times f_{sw} \times (V_{OUT} + V_D)} \\
&= \frac{15 \times (150 + 1.5 - 15)}{0.74 \times 114 \times 10^3 \times (150 + 1.5)} \\
&= 160~\mathrm{\mu H}
\end{aligned}
L = Δ I L ( P − P ) × f s w × ( V O U T + V D ) V I N × ( V O U T + V D − V I N ) = 0.74 × 114 × 1 0 3 × ( 150 + 1.5 ) 15 × ( 150 + 1.5 − 15 ) = 160 μ H
以上の計算からインダクタのインダクタンスL L L L = 200 μ H L = 200 ~\mu H L = 200 μ H
昇圧コンバーターをブレッドボード上に試作する コントローラはMB3759(富士通製TL494のセカンドソース) ダイオードはER504(ファストリカバリーダイオード) インダクタにトロイダルコイル 100μH9Aを2つ接続して200 μ H 200 \mathrm{\mu H} 200 μ H 負荷にin-9を13本接続
実験回路 インダクタ TK30J25D / 東芝製NチャネルMOSFET スイッチング素子: TK30J25D
ゲート入力電荷量 Q g = 100 n C ( V D D = 200 V , V G S = 10 V , I D = 30 A ) Q_g = 100 \mathrm{nC} ~~ (V_{DD} = 200 \mathrm V, V_{GS} = 10 \mathrm V, I_D = 30 \mathrm A) Q g = 100 nC ( V DD = 200 V , V GS = 10 V , I D = 30 A ) オン抵抗 R D S ( O N ) = 0.046 Ω R_{DS(ON)} = 0.046 \mathrm \Omega R D S ( ON ) = 0.046 Ω 入力15.05V, 出力 151V, 134mA, だいたい 20W
ゲート抵抗 R g = 10 Ω R_g = 10 \Omega R g = 10Ω
MB3759のタイミングキャパシタ C T = 2200 p F C_T = 2200 \mathrm{pF} C T = 2200 pF
MB3759のタイミング抵抗 R T = 4.7 k Ω R_T = 4.7 \mathrm{k \Omega} R T = 4.7 kΩ
スイッチング周波数f o s c = 1.2 4.7 × 0.0022 = 116 k H z f_{osc} = \frac{1.2}{4.7 \times 0.0022} = 116 \mathrm{kHz} f osc = 4.7 × 0.0022 1.2 = 116 kHz
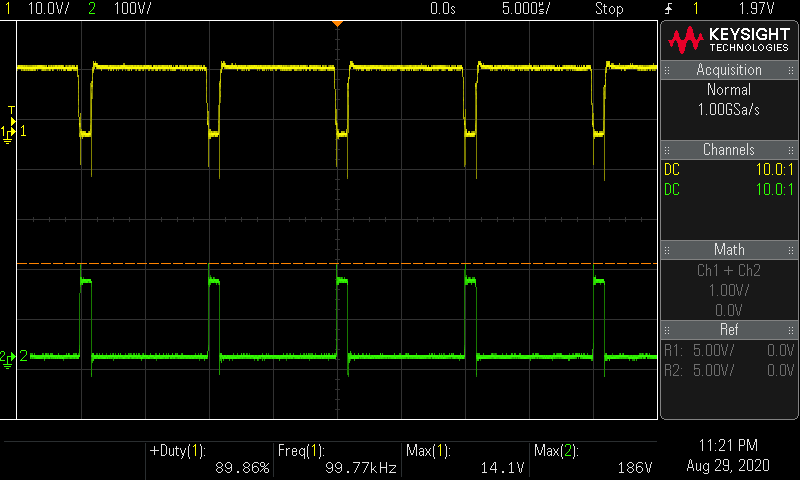
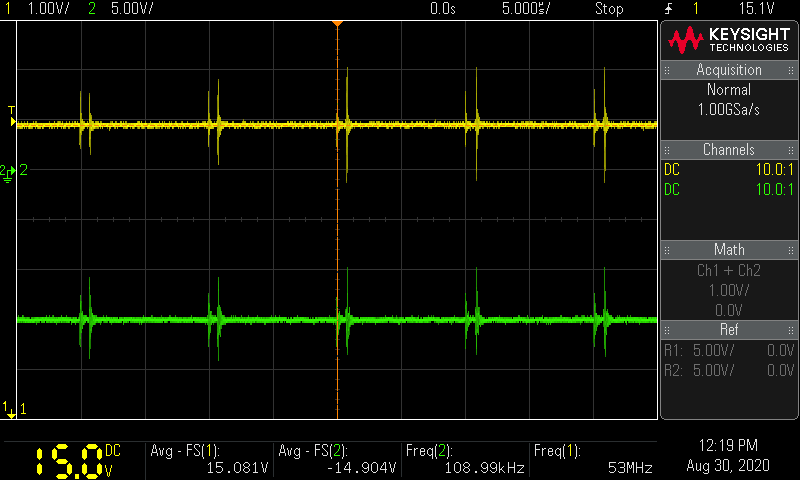
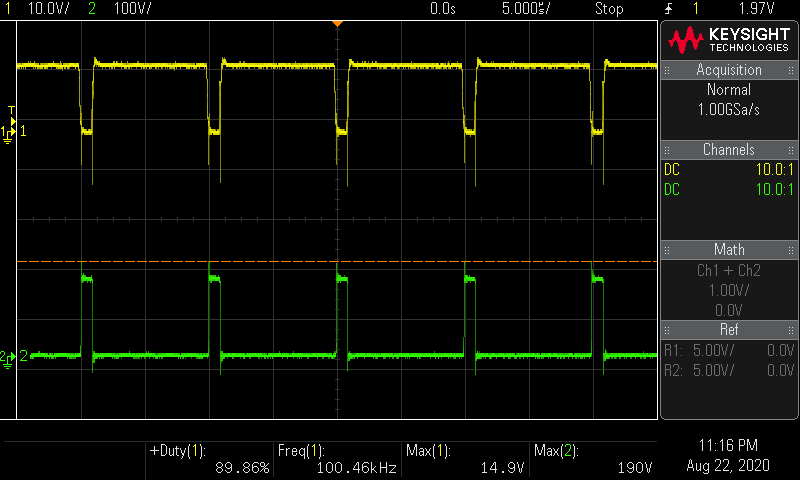
ch.1 MOSFETのゲート波形
ch.2 MOSFETのドレイン波形
結果
V i n = 15.05 V V_{in} = 15.05 \mathrm V V in = 15.05 V I i n = 1.93 A I_{in} = 1.93 \mathrm A I in = 1.93 A P i n = 15.05 × 1.93 = 29.05 W P_{in} = 15.05 \times 1.93 = 29.05 \mathrm W P in = 15.05 × 1.93 = 29.05 W V o u t = 150 V V_{out} = 150 \mathrm V V o u t = 150 V I o u t = 0.135 A I_{out} = 0.135 \mathrm A I o u t = 0.135 A P o u t = 150 × 0.135 = 20.25 W P_{out} = 150 \times 0.135 = 20.25 \mathrm W P o u t = 150 × 0.135 = 20.25 W 効率 η = P o u t ÷ P i n = 20.25 ÷ 29.05 = 0.70 \eta = P_{out} \div P_{in} = 20.25 \div 29.05 = 0.70 η = P o u t ÷ P in = 20.25 ÷ 29.05 = 0.70 効率70%は雑に決めた値が当たった。
インダクタは触れられないくらいの温度になるがヒートシンクはまだ触れられる。
損失 P d = R D S ( O N ) ⋅ I a v g = 0.046 × 1.93 A = 88.8 m W
\begin{aligned}
P_d &= R_{DS(ON)} \cdot I_{avg} \\
&= 0.046 \times 1.93 \mathrm A \\
&= 88.8 \mathrm {mW}
\end{aligned}
P d = R D S ( ON ) ⋅ I a vg = 0.046 × 1.93 A = 88.8 mW
ゲートドライブ電力 P d g = Q g ⋅ V G S ⋅ f s w P d g = 100 × 1 0 − 9 × 15 × 116 × 1 0 3 = 174 m W
\begin{aligned}
P_{dg} &= Q_g \cdot V_{GS} \cdot f_{sw} \\
P_{dg} &= 100 \times 10 ^ {-9} \times 15 \times 116 \times 10^{3} \\
&= 174 \mathrm {mW}
\end{aligned}
P d g P d g = Q g ⋅ V GS ⋅ f s w = 100 × 1 0 − 9 × 15 × 116 × 1 0 3 = 174 mW
うーん。チェンジ
TK13E25D / 東芝製NチャネルMOSFET スイッチング素子: TK13E25D
ゲート入力電荷量 Q g = 25 n C ( V D D = 200 V , V G S = 10 V , I D = 13 A ) Q_g = 25 \mathrm{nC} ~~ (V_{DD} = 200 \mathrm V, V_{GS} = 10 \mathrm V, I_D = 13 \mathrm A) Q g = 25 nC ( V DD = 200 V , V GS = 10 V , I D = 13 A )
オン抵抗 R D S ( O N ) = 0.19 Ω R_{DS(ON)} = 0.19 \mathrm \Omega R D S ( ON ) = 0.19 Ω
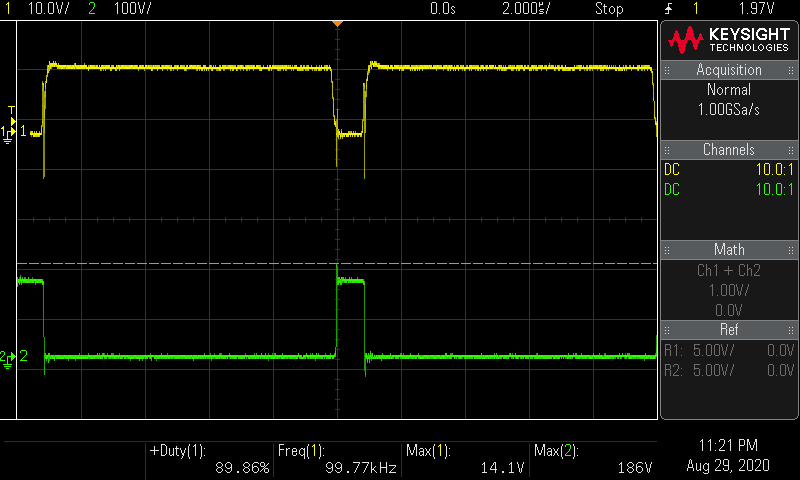
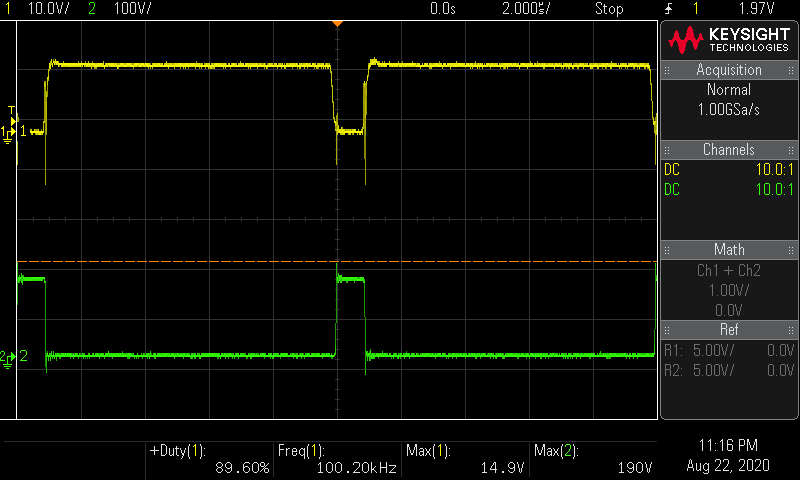
ch.1 MOSFETのゲート波形
ch.2 MOSFETのドレイン波形
結果
V i n = 15.05 V V_{in} = 15.05 \mathrm V V in = 15.05 V I i n = 1.90 A I_{in} = 1.90 \mathrm A I in = 1.90 A P i n = 15.05 × 1.90 = 28.6 W P_{in} = 15.05 \times 1.90 = 28.6 \mathrm W P in = 15.05 × 1.90 = 28.6 W V o u t = 150 V V_{out} = 150 \mathrm V V o u t = 150 V I o u t = 0.134 A I_{out} = 0.134 \mathrm A I o u t = 0.134 A P o u t = 150 × 0.135 = 20.1 W P_{out} = 150 \times 0.135 = 20.1 \mathrm W P o u t = 150 × 0.135 = 20.1 W 効率 η = P o u t ÷ P i n = 20.1 ÷ 28.6 = 0.70 \eta = P_{out} \div P_{in} = 20.1 \div 28.6 = 0.70 η = P o u t ÷ P in = 20.1 ÷ 28.6 = 0.70 損失 P d = 0.19 × 1.90 A = 361 m W
\begin{aligned}
P_d &= 0.19 \times 1.90 \mathrm A \\
&= 361 \mathrm {mW}
\end{aligned}
P d = 0.19 × 1.90 A = 361 mW
ゲートドライブ電力 P d g = 25 × 1 0 − 9 × 15 × 116 × 1 0 3 = 43.5 m W
\begin{aligned}
P_{dg} &= 25 \times 10 ^ {-9} \times 15 \times 116 \times 10^{3} \\
&= 43.5 \mathrm {mW}
\end{aligned}
P d g = 25 × 1 0 − 9 × 15 × 116 × 1 0 3 = 43.5 mW
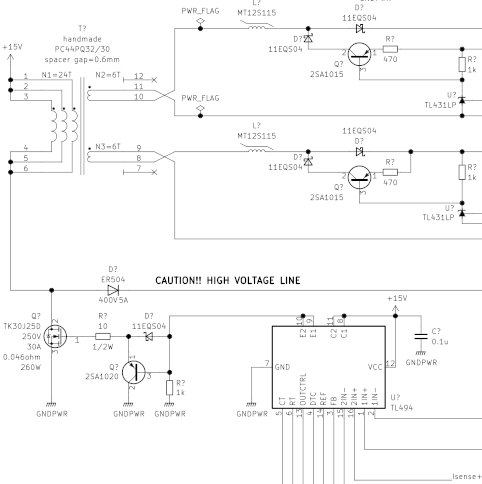
トランス設計 ここから本来の目的である正負15V電源の設計。
トランス1次側はMB3759で安定化しているので, トランス2次側の非安定化出力を可飽和リアクトル(マグアンプ)で安定化する。
swps schematic 計算からトランスの1次側インダクタンスは L = 200 μ H L = 200 \mu H L = 200 μ H
入力電圧 V i n : 15 V V_{in} : 15 \mathrm{V} V in : 15 V 出力電圧(非絶縁, in-9用) V o u t 1 : 150 V V_{out1} : 150 \mathrm{V} V o u t 1 : 150 V 出力電圧(入出力間絶縁, ヘッドホンアンプ用) V o u t 2 : + 15 V , 0.3 A V_{out2} : +15 \mathrm{V}, 0.3 \mathrm{A} V o u t 2 : + 15 V , 0.3 A 出力電圧(入出力間絶縁, ヘッドホンアンプ用) V o u t 3 : − 15 V , 0.3 A V_{out3} : -15 \mathrm{V}, 0.3 \mathrm{A} V o u t 3 : − 15 V , 0.3 A 出力電圧 V o u t : 150 V V_{out} : 150 \mathrm{V} V o u t : 150 V ダイオードの順方向電圧 V F : 1.5 V V_F : 1.5 \mathrm{V} V F : 1.5 V 出力電力 P o : 30 W P_o: 30 \mathrm{W} P o : 30 W 効率 η : 70 \eta : 70 η : 70 スイッチング周波数 f s w : 116 k H z f_{sw} : 116 \mathrm{kHz} f s w : 116 kHz 通流率(Duty cycle) D : 0.93 D : 0.93 D : 0.93 インダクタのインダクタンス L : 200 μ H L : 200 \mu H L : 200 μ H TDK PC44PQ32/30コア を使いますが,
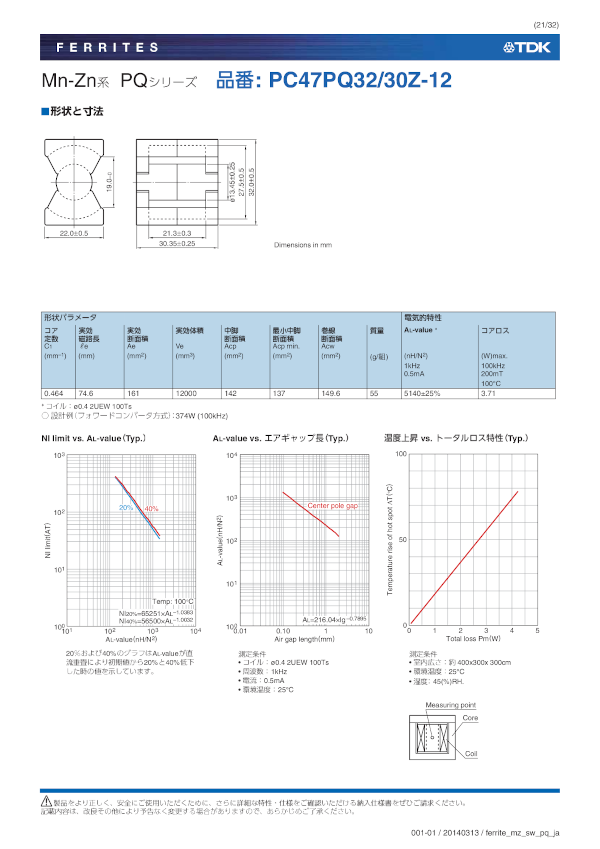
出典: TDK PC47PQ32/30コアのデーターシート PC47PQ32/30Z 性能諸元
実効断面積 A e = 161 m m 2 A_e = 161 ~\mathrm{mm^2} A e = 161 m m 2 AL値(ギャップ付) A L value = 160 n H / N 2 AL_\text{value} = 160 ~\mathrm{nH / N^2} A L value = 160 nH/ N 2 一次側巻線数Npの算出 A L value = 200 n H / t u r n s 2 AL_\text{value} = 200~\mathrm{nH / turns^2} A L value = 200 nH/turn s 2
N p = L p A L value = 200 μ H 200 n H / t u r n s 2 = 200 μ H 0.2 μ H / t u r n s 2 = 31.6 t u r n s ⇒ N p は32ターン
\begin{aligned}
N_p &= \sqrt{\frac{L_p}{AL_\text{value}}} \\
&= \sqrt{\frac{200 ~\mathrm{\mu H}}{200 ~\mathrm{nH / turns^2}}} \\
&= \sqrt{\frac{200 ~\mathrm{\mu H}}{0.2 ~\mathrm{\mu H / turns^2}}} \\
&= 31.6 ~\mathrm{turns} \\
&\Rightarrow {N_p\text{は32ターン}}
\end{aligned}
N p = A L value L p = 200 nH/turn s 2 200 μ H = 0.2 μ H/turn s 2 200 μ H = 31.6 turns ⇒ N p は 32 ターン
L p = 200 μ H = 200000 n H N p = 32 t u r n s A L value = 200000 / 3 2 2 = 195.3 n H / t u r n s 2 N I = N p × I p p k = 32 t u r n s × 3.377 A = 108.064 A ⋅ t u r n s
\begin{aligned}
L_p &= 200 ~ \mathrm{\mu H} = 200 000 ~ \mathrm{nH}\
N_p &= 32 ~ \mathrm{turns} \
AL_\text{value} &= 200 000 / 32^2 = 195.3 ~ \mathrm{nH / turns^2} \
NI &= N_p \times I_ppk \
&= 32~\mathrm{turns} \times 3.377~\mathrm{A} \
&= 108.064~\mathrm{A \cdot turns}
\end{aligned}
L p = 200 μ H = 200000 nH N p = 32 turns A L value = 200000/3 2 2 = 195.3 nH/turn s 2 N I = N p × I p p k = 32 turns × 3.377 A = 108.064 A ⋅ turns
出典: TDK PC47PQ32/30コアのデーターシート うーん。もうちょっと。
A L value = 400 n H / t u r n s 2 AL_\text{value} = 400~\mathrm{nH / turns^2} A L value = 400 nH/turn s 2
N p = L p A L value = 200 μ H 400 n H / t u r n s 2 = 200 μ H 0.4 μ H / t u r n s 2 = 22.4 t u r n s ⇒ N p は23ターン
\begin{aligned}
N_p &= \sqrt{\frac{L_p}{AL_\text{value}}} \\
&= \sqrt{\frac{200 ~\mathrm{\mu H}}{400 ~\mathrm{nH / turns^2}}} \\
&= \sqrt{\frac{200 ~\mathrm{\mu H}}{0.4 ~\mathrm{\mu H / turns^2}}} \\
&= 22.4 ~\mathrm{turns} \\
&\Rightarrow {N_p\text{は23ターン}}
\end{aligned}
N p = A L value L p = 400 nH/turn s 2 200 μ H = 0.4 μ H/turn s 2 200 μ H = 22.4 turns ⇒ N p は 23 ターン
L p = 200 μ H = 200000 n H N p = 23 t u r n s A L value = 200000 / 2 3 2 = 378 n H / t u r n s 2 N I = N p × I p p k = 23 t u r n s × 3.377 A = 77.671 A ⋅ t u r n s
\begin{aligned}
L_p &= 200 ~ \mathrm{\mu H} = 200 000 ~ \mathrm{nH}\
N_p &= 23 ~ \mathrm{turns} \
AL_\text{value} &= 200 000 / 23^2 = 378 ~ \mathrm{nH / turns^2} \
NI &= N_p \times I_ppk \
&= 23~\mathrm{turns} \times 3.377~\mathrm{A} \
&= 77.671~\mathrm{A \cdot turns}
\end{aligned}
L p = 200 μ H = 200000 nH N p = 23 turns A L value = 200000/2 3 2 = 378 nH/turn s 2 N I = N p × I p p k = 23 turns × 3.377 A = 77.671 A ⋅ turns
出典: TDK PC47PQ32/30コアのデーターシート これでいいや。
二次側巻線数Ns1, Ns2の算出 とりあえず N s 1 = N s 2 = 6 t u r n s N_{s1} = N_{s2} = 6~\mathrm{turns} N s 1 = N s 2 = 6 turns
トランス設計(構造設計) 資料
ボビンの選定 CPV-PQ32/30 を使うことにする。
有効巻枠の確認 巻き幅 18.67mm 巻き高さ (26.57mm - 13.97mm) / 2 = 6.3mm 沿面距離とバリアテープ 動作電圧: 200V 汚染度合: 2 材料群:Ⅲa(CTI<400) IEC60950に基づく必要な最低沿面距離 ボビンの有効巻き幅は上下のバリアテープの幅を2mm,4mm確保して 18.67 − 2.0 − 4.0 = 12.67 m m 18.67 - 2.0 - 4.0 = 12.67 \mathrm{mm} 18.67 − 2.0 − 4.0 = 12.67 mm
線材の選定 ここから資料
計算がめんどくさくなったので, トランスの一次側電流はだいたい 4 A 4 \mathrm A 4 A
一次側巻き線線径(3並列) 線径 = 2 × 実効電流 巻線本数 × π × 電流密度
\text{線径} = 2 \times \sqrt{\frac{\text{実効電流}}{\text{巻線本数} \times \pi \times \text{電流密度}}}
線径 = 2 × 巻線本数 × π × 電流密度 実効電流
今回は電流密度は 7 A / m m 2 7~\mathrm{A/mm^2} 7 A/m m 2
ϕ N p = 2 × 4 3 × π × 7 = 0.49 m m
\phi_{Np} = 2 \times \sqrt{\frac{4}{3 \times \pi \times 7}} = 0.49 \mathrm{mm}
ϕ Np = 2 × 3 × π × 7 4 = 0.49 mm
となるので, 使用線材はマグネットワイヤ 2種UEW0.5mm(最大仕上がり外形 0.542mm)とする。
12.67 0.542 × 1.01 = 23 t u r n s
\frac{12.67}{0.542 \times 1.01} = 23 \mathrm{turns}
0.542 × 1.01 12.67 = 23 turns
丁度よろしい。
二次側巻き線線径 使用線材は2UEW0.6mmとする。
トランス仕様決定 23turnsを3で割ると半端が出る加減で4層に分割する。
1層目: 1次側, UEW0.5, 6回巻き, 3並列巻線 2層目: 1次側, UEW0.5, 6回巻き, 3並列巻線 3層目: 1次側, UEW0.5, 6回巻き, 3並列巻線 4層目: 1次側, UEW0.5, 6回巻き, 3並列巻線 5層目: 2次側, UEW0.6, 6回巻き, 2セット すべての巻き線は上から見て時計回りの方向に巻く。
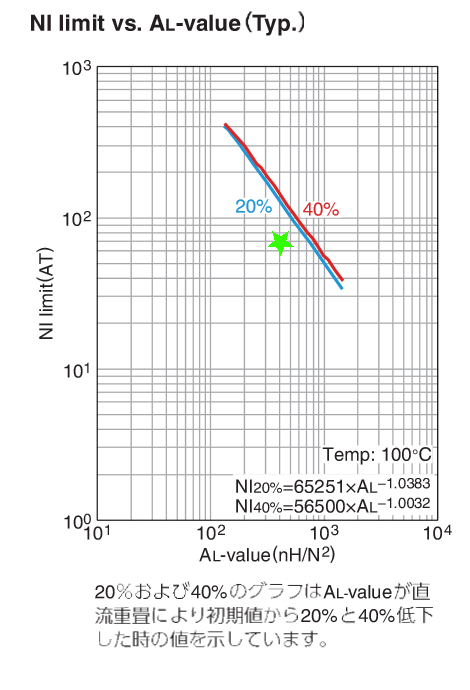
ギャップ長の算出 N p = 24 t u r n s N_p = 24 \mathrm{turns} N p = 24 turns L p = 200 μ H = 200000 n H L_p = 200 \mathrm{\mu H} = 200000 \mathrm{nH} L p = 200 μ H = 200000 nH A L value = L p N p 2 = 200000 2 4 2 = 347 n H / t u r n s 2
\begin{aligned}
AL_\text{value} &= \frac{L_p}{ {N_p} ^ 2 } \\
&= \frac{200000}{ 24 ^ 2 } \\
&= 347 \mathrm{nH / turns^2}
\end{aligned}
A L value = N p 2 L p = 2 4 2 200000 = 347 nH/turn s 2
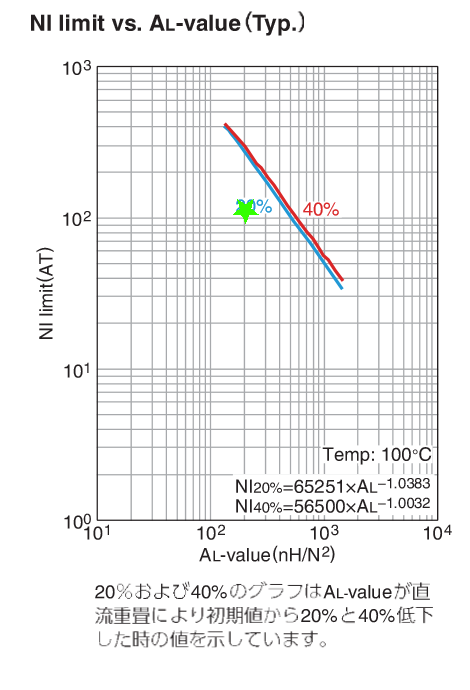
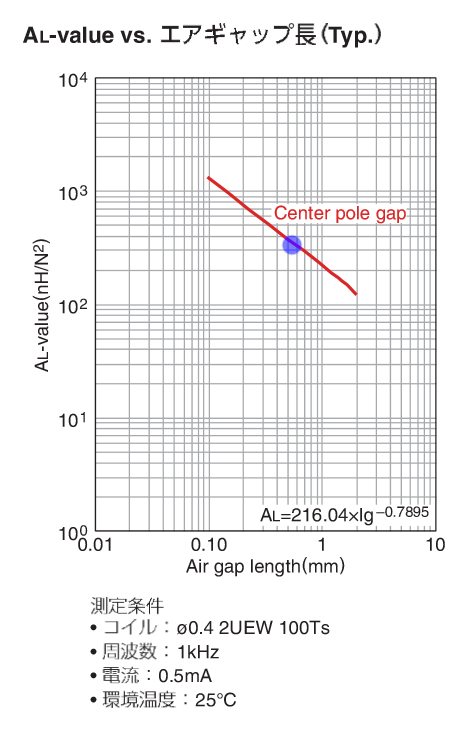
なのでAL-value vs エアギャップ長のグラフから
出典: TDK PC47PQ32/30コアのデーターシート いちおう計算すると μ 0 = 4 π × 1 0 − 7 \mu_0 = 4 \pi \times 10^{-7} μ 0 = 4 π × 1 0 − 7
ℓ g = μ 0 × A e × N p 2 L = 4 π × 1 0 − 7 × 161 × 1 0 − 6 × 2 4 2 200 × 1 0 − 6 = 4 π × 161 × 2 4 2 200 × 1 0 − 7 × 1 0 − 6 1 0 − 6 = 370944 200 π × 1 0 − 7 × 1 0 − 6 1 0 − 6 = 1855 × π × 1 0 − 7 = 5828 × 1 0 − 4 × 1 0 − 3 = 0.58 × 1 0 − 3 m = 0.58 m m (Center pole gap) , 0.29 m m (Spacer gap)
\begin{aligned}
\ell_g &= \frac{\mu_0 \times A_e \times N_p ~ ^2}{L} \\
&= \frac{4 \pi \times 10^{-7} \times 161 \times 10^{-6} \times 24^2}{200 \times 10^{-6}} \\
&= \frac{4 \pi \times 161 \times 24^2}{200} \times \frac{10^{-7} \times 10^{-6}}{10^{-6}} \\
&= \frac{370944}{200} \pi \times \frac{10^{-7} \times \cancel{10^{-6}}}{\cancel{10^{-6}}} \\
&= 1855 \times \pi \times 10^{-7} \\
&= 5828 \times 10^{-4} \times 10^{-3}\\
&= 0.58 \times 10^{-3} ~\mathrm{m} \\
&= 0.58 ~\mathrm{mm} ~ \text{(Center pole gap)}, 0.29 ~\mathrm{mm} ~ \text{(Spacer gap)}
\end{aligned}
ℓ g = L μ 0 × A e × N p 2 = 200 × 1 0 − 6 4 π × 1 0 − 7 × 161 × 1 0 − 6 × 2 4 2 = 200 4 π × 161 × 2 4 2 × 1 0 − 6 1 0 − 7 × 1 0 − 6 = 200 370944 π × 1 0 − 6 1 0 − 7 × 1 0 − 6 = 1855 × π × 1 0 − 7 = 5828 × 1 0 − 4 × 1 0 − 3 = 0.58 × 1 0 − 3 m = 0.58 mm (Center pole gap) , 0.29 mm (Spacer gap)
「ポリエステルフィルム粘着テープ No.631S #25 黄色 」の厚みは0.05mmなので0.29 ÷ 0.05 = 5.8 0.29 \div 0.05 = 5.8 0.29 ÷ 0.05 = 5.8
トランス製作 バリアテープは「コンビネーション粘着テープ673F 0.27 」をポリエステルフィルム粘着テープ No.631S #25 黄色 」を
bobbin 第1層はじめ(1次側) 第1層おわり(1次側) 第2層はじめ(1次側) 第3層はじめ(1次側) 第4層はじめ(1次側) 第5層おわり(2次側) 第5層裏側 巻き線おわり コア 組み立てた 組み立てた てきとうに選んだコアだからか巻き線スペースがもう1層できるくらい余ってしまった。
インダクタンス測定
インダクタンス測定 製作したトランスの1次側インダクタンスをLCRメータで測定すると 217.3 μ H 217.3 ~ \mathrm{\mu H} 217.3 μ H
直流抵抗測定 0.134 Ω 0.134 \Omega 0.134Ω R = 0.134 ÷ 3 = 0.05 Ω R = 0.134 \div 3 = 0.05 \Omega R = 0.134 ÷ 3 = 0.05Ω
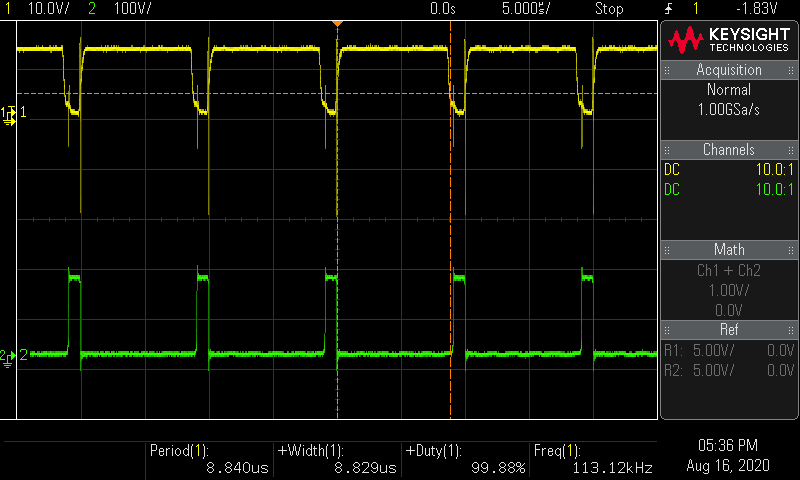
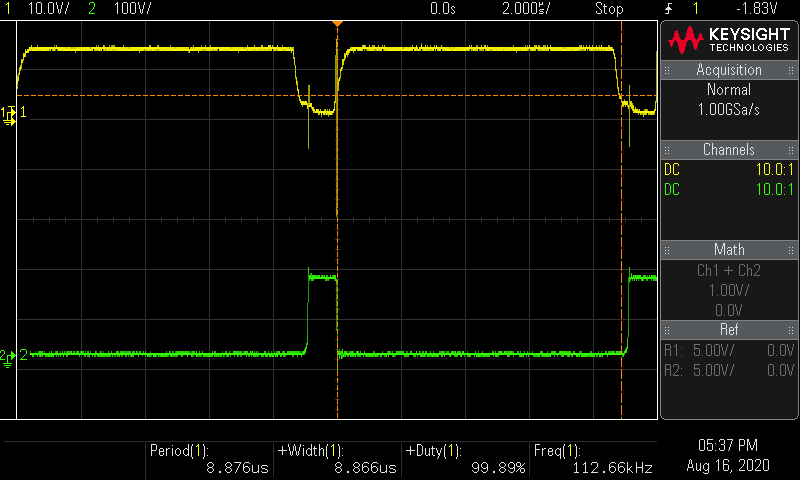
製作したトランスで昇圧コンバーターをブレッドボード上に試作する スイッチング素子: TK13E25D
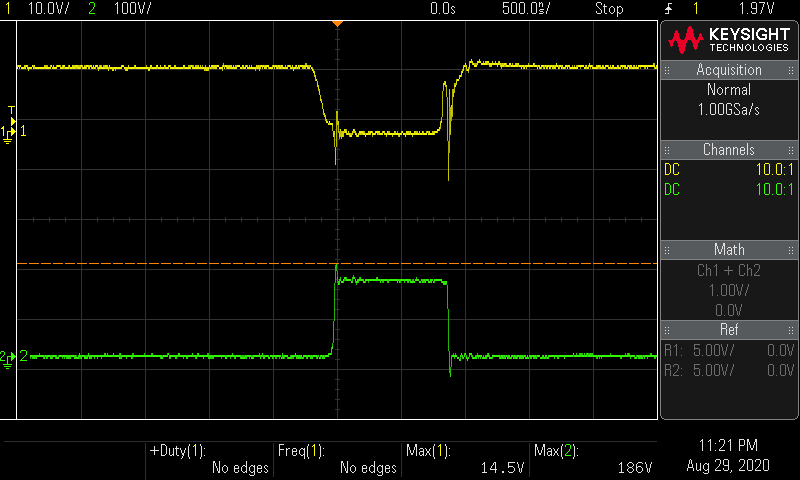
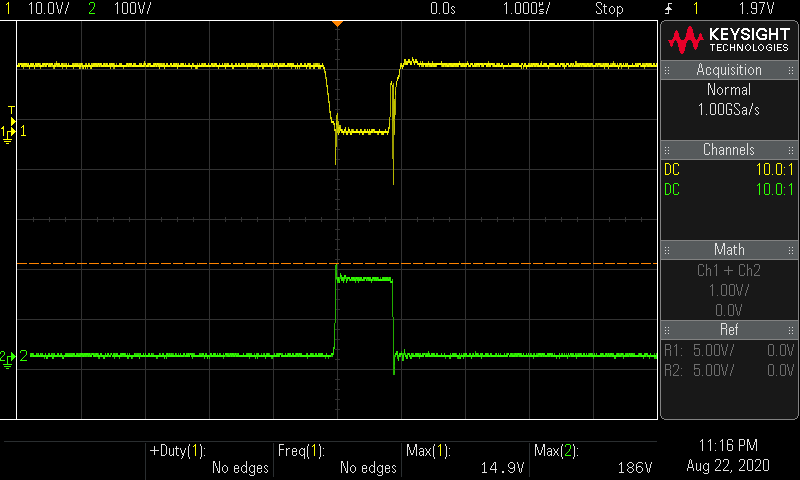
ch.1 MOSFETのゲート波形 ch.2 MOSFETのドレイン波形
結果
V i n = 15.05 V V_{in} = 15.05 \mathrm V V in = 15.05 V I i n = 1.70 A I_{in} = 1.70 \mathrm A I in = 1.70 A P i n = 15.05 × 1.70 = 25.6 W P_{in} = 15.05 \times 1.70 = 25.6 \mathrm W P in = 15.05 × 1.70 = 25.6 W V o u t = 150.6 V V_{out} = 150.6 \mathrm V V o u t = 150.6 V I o u t = 0.136 A I_{out} = 0.136 \mathrm A I o u t = 0.136 A P o u t = 150.6 × 0.136 = 20.5 W P_{out} = 150.6 \times 0.136 = 20.5 \mathrm W P o u t = 150.6 × 0.136 = 20.5 W 効率 η = P o u t ÷ P i n = 20.5 ÷ 25.6 = 0.80 \eta = P_{out} \div P_{in} = 20.5 \div 25.6 = 0.80 η = P o u t ÷ P in = 20.5 ÷ 25.6 = 0.80 効率 η = 80 \eta = 80 % η = 80
電源装置をブレッドボード上に試作する こんな感じです。
スイッチング素子: TK13E25D
150V出力しながら, +-15V正負両電源もきちんと制御できている。
巨人版ヘッドホンアンプキットを接続して音を聞いてみると
しかしながら無音の時のノイズが気になる。
昇圧コンバーターの回路トポロジーの関係で放熱板がホットエンドになるし, トランスにショートリングを入れていないから漏れ磁束が周囲の電線と鎖交しているでしょうね。
出典: Application Report SLVA372C1
出典: CPV-PQ32/30-1S-12P-Z Drawing
 製作したトランスの1次側抵抗は1巻線を代表ではかると となった。
それが3並列あるので となる(はず)。
製作したトランスの1次側抵抗は1巻線を代表ではかると となった。
それが3並列あるので となる(はず)。