単電源入力, 正負両電源出力のDCDCコンバータを自作しようかと考えて
絶縁型フライバックコンバータ回路設計:トランス設計(数値算出)
リンクの記事を参考にして設計を始める。
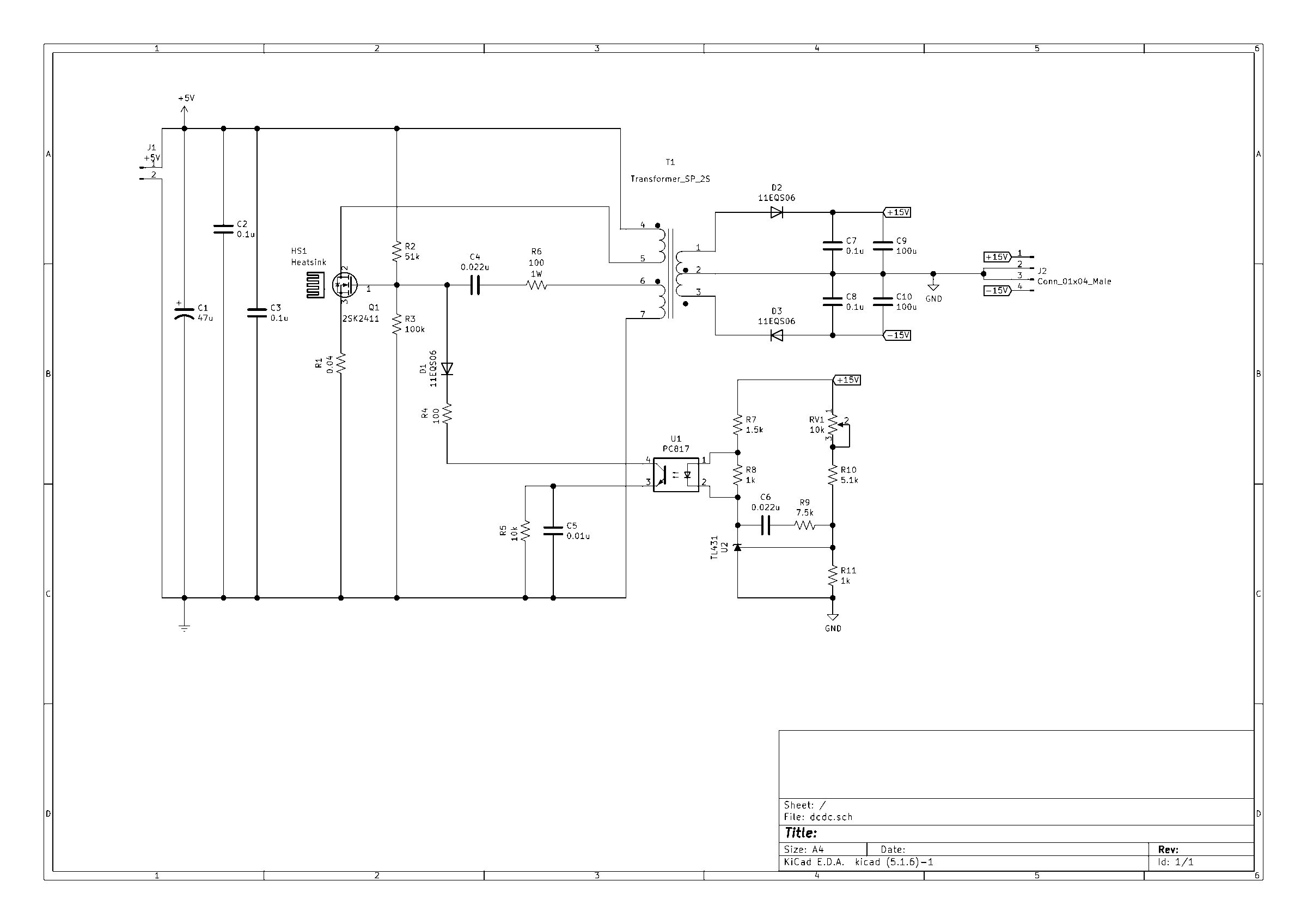
実験回路図 使う部品の少ない自励型DCDCコンバータを適当に設計してみた。
トランス設計(数値算出) 仕様
入力電圧 V i n : 4.5 ~ 5.0 V V_{in} : 4.5 \text{~} 5.0 \mathrm{V} V in : 4.5 ~ 5.0 V 出力電圧 V o u t : ± 15 V V_{out} : \pm 15 \mathrm{V} V o u t : ± 15 V 出力電流 I o u t : 300 m A I_{out} : 300~\mathrm{mA} I o u t : 300 mA 出力電力 P o : 30 V × 0.3 A = 9 W P_o : 30\mathrm{V} \times 0.3\mathrm{A} = 9~\mathrm{W} P o : 30 V × 0.3 A = 9 W 制御電圧 V d : 10 V V_d : 10~\mathrm{V} V d : 10 V ダイオードの順方向電圧 V F : 1.0 V V_F : 1.0~\mathrm{V} V F : 1.0 V 周波数 f s w m a x : 40 k H z f_{sw}max : 40~\mathrm{kHz} f s w ma x : 40 kHz 絶縁型フライバックコンバータ回路設計:トランス設計(数値算出) | 電源設計の技術情報サイトのTechWeb
フライバック電圧VORの設定 正負電圧出力であることを考えて V O V_O V O
V o = V o u t + V F = ( 15 + 1 ) + ( − 15 − 1 ) = 32 V
\begin{aligned}
V_o &= V_{out} + V_F \\
&= (15 + 1) + (-15 - 1) \\
&= 32~\mathrm{V}
\end{aligned}
V o = V o u t + V F = ( 15 + 1 ) + ( − 15 − 1 ) = 32 V
として
今回は V O R = 4 VOR = 4 V OR = 4
N p N s = V O R V o = 4 32 = 0.125
\begin{aligned}
\frac{N_p}{N_s} &= \frac{VOR}{V_o} \\
&= \frac{4}{32} \\
&= 0.125 \\
\end{aligned}
N s N p = V o V OR = 32 4 = 0.125
D u t y ( m a x ) = V O R V i n ( m i n ) + V O R = 4 4.5 + 4 = 0.47
\begin{aligned}
Duty(max) &= \frac{VOR}{V_{in}(min) + VOR} \\
&= \frac{4}{4.5+4} \\
&= 0.47
\end{aligned}
D u t y ( ma x ) = V in ( min ) + V OR V OR = 4.5 + 4 4 = 0.47
となる。
二次側巻線インダクタンスLs、二次側の最大電流Ispkの算出 最大負荷電流 I o m a x I_{o}max I o ma x
I o m a x = 1.2 × I o u t = 1.2 × 0.3 = 0.36 A
\begin{aligned}
I_{o}max &= 1.2 \times I_{out} \\
&= 1.2 \times 0.3 \\
&= 0.36 ~\mathrm{A}
\end{aligned}
I o ma x = 1.2 × I o u t = 1.2 × 0.3 = 0.36 A
L s < ( V o u t + V F ) × ( 1 − D u t y ) 2 2 × I o m a x × f s w m a x = 32 × ( 1 − 0.47 ) 2 2 × 0.36 × 40 × 1 0 3 = 312 μ H
\begin{aligned}
L_s &< \frac{ (V_{out} + V_F) \times (1- Duty)^2 }{2 \times I_{o}max \times f_{sw}max} \\
&= \frac{32 \times (1 - 0.47)^2}{ 2 \times 0.36 \times 40 \times 10^3} \\
&= 312 ~\mathrm{\mu H}
\end{aligned}
L s < 2 × I o ma x × f s w ma x ( V o u t + V F ) × ( 1 − D u t y ) 2 = 2 × 0.36 × 40 × 1 0 3 32 × ( 1 − 0.47 ) 2 = 312 μ H
I s p k = 2 × I o m a x 1 − D u t y ( m a x ) = 2 × 0.36 1 − 0.47 = 1.36 A
\begin{aligned}
I_{s}pk &= \frac{ 2 \times I_{o}max }{ 1 - Duty(max) } \\
&= \frac{ 2 \times 0.36 }{ 1 - 0.47 } \\
&= 1.36 ~\mathrm{A}
\end{aligned}
I s p k = 1 − D u t y ( ma x ) 2 × I o ma x = 1 − 0.47 2 × 0.36 = 1.36 A
一次側巻線インダクタンスLp、一次側の最大電流Ippkの算出 L p = L s × ( N p N s ) 2 = 312 μ H × 0.12 5 2 = 4.88 μ H
\begin{aligned}
L_p &= L_s \times \left( \frac{N_p}{N_s} \right)^2 \\
&= 312 ~\mathrm{\mu H} \times 0.125^2 \\
&= 4.88 ~\mathrm{\mu H}
\end{aligned}
L p = L s × ( N s N p ) 2 = 312 μ H × 0.12 5 2 = 4.88 μ H
I p p k = I s p k × N s N p = 1.36 × 1 0.125 = 10.88 A
\begin{aligned}
I_{p}pk &= I_{s}pk \times \frac{N_s}{N_p} \\
&= 1.36 \times \frac{1}{0.125} \\
&= 10.88 ~\mathrm{A}
\end{aligned}
I p p k = I s p k × N p N s = 1.36 × 0.125 1 = 10.88 A
トランスサイズの決定 出力電力 P o P_o P o TDK PC44PQ20/16コア を使うことにする。
TDKプロダクトセンター より以下の資料を入手する。
PC44材の資料が見つからないのでPC47材の資料を参考にする。
PC47材 性能諸元
飽和磁束密度 B s a t = 420 mT @ 100 ∘ C B_{sat} = 420~\textrm{mT} @ 100{^\circ\mathrm{C}} B s a t = 420 mT @100 ∘ C
PC47PQ20/16Z 性能諸元
実効断面積 A e = 62 m m 2 A_e = 62 ~\mathrm{mm^2} A e = 62 m m 2 AL値(ギャップ付) A L value = 100 n H / N 2 AL_\text{value} = 100 ~\mathrm{nH / N^2} A L value = 100 nH/ N 2 一次側巻線数Npの算出 資料にあるPC47材と使うPC44材との相違と余裕を見込んで飽和磁束密度B s a t = 0.35 T B_{sat} = 0.35~\mathrm{T} B s a t = 0.35 T
N p > V i n × T o n A e × B s a t = L p × I p p k A e × B s a t = 4.88 μ H × 10.88 A 64 m m 2 × 0.35 T = 4.88 × 1 0 − 6 × 10.88 64 × 1 0 − 6 × 0.35 = 4.88 × 10.88 64 × 0.35 = 2.37 t u r n s ⇒ N p は3ターン以上
\begin{aligned}
N_p &> \frac{V_{in} \times T_{on}}{A_e \times B_{sat}} = \frac{L_p \times I_{p}pk}{A_e \times B_{sat}} \\
&= \frac{4.88 \mathrm{\mu H} \times 10.88 \mathrm{A}}{64 \mathrm{mm^2} \times 0.35 \mathrm{T}} \\
&= \frac{4.88 \times \cancel{10^{-6}} \times 10.88}{64 \times \cancel{10^{-6}} \times 0.35} \\
&= \frac{4.88 \times 10.88}{64 \times 0.35} \\
&= 2.37 ~\mathrm{turns} \\
&\Rightarrow {N_p\text{は3ターン以上}}
\end{aligned}
N p > A e × B s a t V in × T o n = A e × B s a t L p × I p p k = 64 m m 2 × 0.35 T 4.88 μ H × 10.88 A = 64 × 1 0 − 6 × 0.35 4.88 × 1 0 − 6 × 10.88 = 64 × 0.35 4.88 × 10.88 = 2.37 turns ⇒ N p は 3 ターン以上
A L value = 100 n H / t u r n s 2 AL_\text{value} = 100~\mathrm{nH / turns^2} A L value = 100 nH/turn s 2
N p = L p A L value = 4.88 μ H 100 n H / t u r n s 2 = 4.88 μ H 0.1 μ H / t u r n s 2 = 6.98 t u r n s ⇒ N p は7ターン
\begin{aligned}
N_p &= \sqrt{\frac{L_p}{AL_\text{value}}} \\
&= \sqrt{\frac{4.88 ~\mathrm{\mu H}}{100 ~\mathrm{nH / turns^2}}} \\
&= \sqrt{\frac{4.88 ~\mathrm{\mu H}}{0.1 ~\mathrm{\mu H / turns^2}}} \\
&= 6.98 ~\mathrm{turns} \\
&\Rightarrow {N_p\text{は7ターン}}
\end{aligned}
N p = A L value L p = 100 nH/turn s 2 4.88 μ H = 0.1 μ H/turn s 2 4.88 μ H = 6.98 turns ⇒ N p は 7 ターン
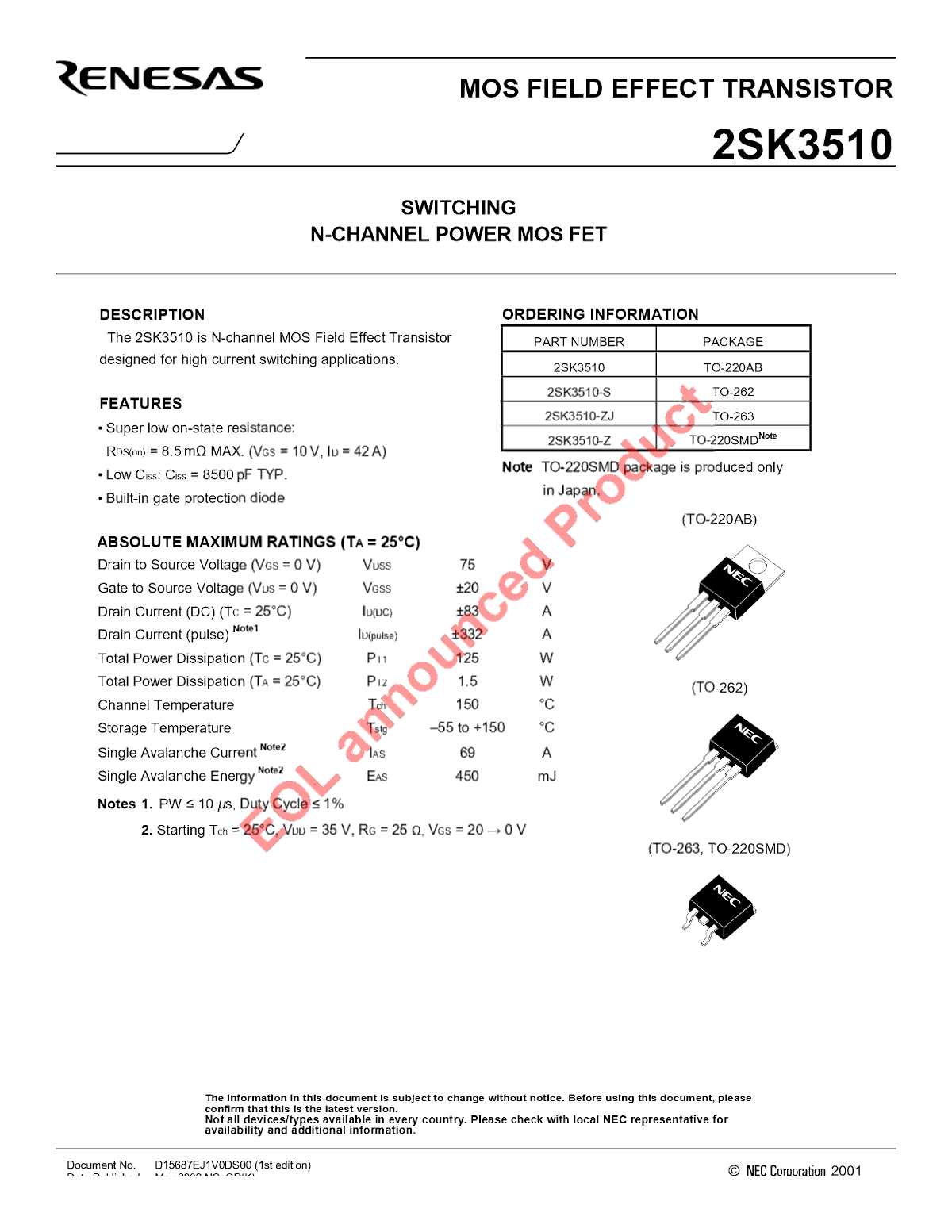
L p = 4.88 μ H = 4880 n H N p = 7 t u r n s A L value = 4880 / 7 2 = 99.59 n H / t u r n s 2 N I = N p × I p p k = 7 t u r n s × 10.88 A = 76.2 A ⋅ t u r n s
\begin{aligned}
L_p &= 4.88 ~ \mathrm{\mu H} = 4880 ~ \mathrm{nH}\
N_p &= 7 ~ \mathrm{turns} \
AL_\text{value} &= 4880 / 7^2 = 99.59 ~ \mathrm{nH / turns^2} \
NI &= N_p \times I_ppk \
&= 7~\mathrm{turns} \times 10.88~\mathrm{A} \
&= 76.2~\mathrm{A \cdot turns}
\end{aligned}
L p = 4.88 μ H = 4880 nH N p = 7 turns A L value = 4880/ 7 2 = 99.59 nH/turn s 2 N I = N p × I p p k = 7 turns × 10.88 A = 76.2 A ⋅ turns
NI-ALvalue01 余裕。あるじゃないですか。
もうちょっと攻めた設計で A L value = 300 n H / t u r n s 2 AL_\text{value} = 300~\mathrm{nH / turns^2} A L value = 300 nH/turn s 2
N p = L p A L value = 4.88 μ H 0.3 μ H / t u r n s 2 = 4.03 t u r n s ⇒ N p は4ターン
\begin{aligned}
N_p &= \sqrt{\frac{L_p}{AL_\text{value}}} \\
&= \sqrt{\frac{4.88 ~\mathrm{\mu H}}{0.3 ~\mathrm{\mu H / turns^2}}} \\
&= 4.03 ~\mathrm{turns} \\
&\Rightarrow {N_p\text{は4ターン}}
\end{aligned}
N p = A L value L p = 0.3 μ H/turn s 2 4.88 μ H = 4.03 turns ⇒ N p は 4 ターン
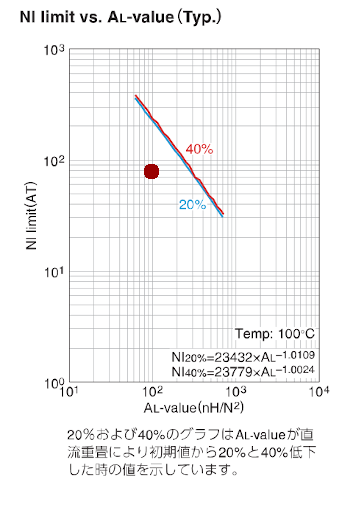
L p = 4.88 μ H = 4880 n H N p = 4 t u r n s A L value = 4880 / 4 2 = 305 n H / t u r n s 2 N I = N p × I p p k = 4 t u r n s × 10.88 A = 43.52 A ⋅ t u r n s
\begin{aligned}
L_p &= 4.88 ~ \mathrm{\mu H} = 4880 ~ \mathrm{nH}\
N_p &= 4 ~ \mathrm{turns} \
AL_\text{value} &= 4880 / 4^2 = 305 ~ \mathrm{nH / turns^2} \
NI &= N_p \times I_ppk \
&= 4 ~\mathrm{turns} \times 10.88~\mathrm{A} \
&= 43.52 ~\mathrm{A \cdot turns}
\end{aligned}
L p = 4.88 μ H = 4880 nH N p = 4 turns A L value = 4880/ 4 2 = 305 nH/turn s 2 N I = N p × I p p k = 4 turns × 10.88 A = 43.52 A ⋅ turns
NI-ALvalue02 もっと頑張れそうだが、PC44材の代わりにPC47材の資料を見ているのでもうこれでいいことにする。
二次側巻線数Nsの算出 最初に決めた値である N p N s = 0.125 \frac{N_p}{N_s} = 0.125 N s N p = 0.125 N s = N p 0.125 = 4 0.125 = 32 t u r n s
\begin{aligned}
N_s &= \frac{N_p}{0.125} \\
&= \frac{4}{0.125} \\
&= 32 ~\mathrm{turns} \\
\end{aligned}
N s = 0.125 N p = 0.125 4 = 32 turns
N s N_s N s
VCC巻線数Ndの算出 これは大雑把に V C C + V F V C C = 10 V V_{CC} + V_{FVCC} = 10 ~\mathrm{V} V CC + V F V CC = 10 V
N d = N s × V C C + V F V C C V o u t + V F = 32 × 10 32 = 10 t u r n s
\begin{aligned}
N_d &= N_s \times \frac{V_{CC} + V_{FVCC}}{V_{out} + V_F} \\
&= 32 \times \frac{10}{32} \\
&= 10 ~\mathrm{turns}
\end{aligned}
N d = N s × V o u t + V F V CC + V F V CC = 32 × 32 10 = 10 turns
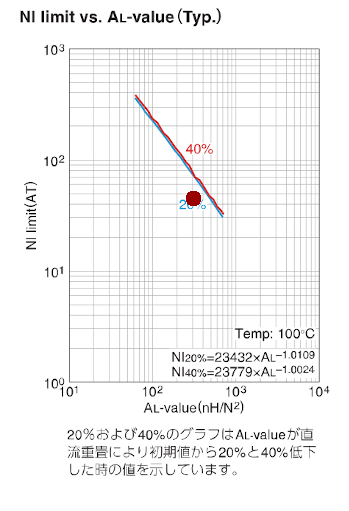
ギャップ長の算出 A L value = 305 n H / t u r n s 2 AL_\text{value} = 305 ~ \mathrm{nH / turns^2} A L value = 305 nH/turn s 2 2 )とエアギャップ長(Typ.)の交差点から下に線を引いて
ALvalue-gap01 ギャップ長 ℓ g = 0.2 ~ 0.3 mm (Center pole gap) \ell_g = 0.2 \text{~} 0.3 ~\textrm{mm} ~ \text{(Center pole gap)} ℓ g = 0.2 ~ 0.3 mm (Center pole gap)
計算で求めると(真空の透磁率μ 0 = 4 π × 1 0 − 7 \mu_0 = 4 \pi \times 10^{-7} μ 0 = 4 π × 1 0 − 7
ℓ g = μ 0 × A e × N p 2 L = 4 π × 1 0 − 7 × 62 × 1 0 − 6 × 4 2 4.88 × 1 0 − 6 = 4 π × 62 × 4 2 4.88 × 1 0 − 7 × 1 0 − 6 1 0 − 6 = 4 π × 62 × 4 2 4.88 × 1 0 − 7 × 1 0 − 6 1 0 − 6 = π × 62 × 4 × 4 1.22 × 1 0 − 7 = 992 1.22 π × 1 0 − 4 × 1 0 − 3 = 992 1.22 π × 1 10000 × 1 0 − 3 = 992 12200 π × 1 0 − 3 = 0.255 × 1 0 − 3 m = 0.26 m m (Center pole gap)
\begin{aligned}
\ell_g &= \frac{\mu_0 \times A_e \times N_p ~ ^2}{L} \\
&= \frac{4 \pi \times 10^{-7} \times 62 \times 10^{-6} \times 4^2}{4.88 \times 10^{-6}} \\
&= \frac{4 \pi \times 62 \times 4^2}{4.88} \times \frac{10^{-7} \times 10^{-6}}{10^{-6}} \\
&= \frac{\cancel{4} \pi \times 62 \times 4^2}{\cancel{4.88}} \times \frac{10^{-7} \times \cancel{10^{-6}}}{\cancel{10^{-6}}} \\
&= \frac{\pi \times 62 \times 4 \times 4}{1.22} \times 10^{-7} \\
&= \frac{992}{1.22} \pi \times 10^{-4} \times 10^{-3}\\
&= \frac{992}{1.22} \pi \times \frac{1}{10000} \times 10^{-3}\\
&= \frac{992}{12200} \pi \times 10^{-3}\\
&= 0.255 \times 10^{-3} ~\mathrm{m} \\
&= 0.26 ~\mathrm{mm} ~ \text{(Center pole gap)}
\end{aligned}
ℓ g = L μ 0 × A e × N p 2 = 4.88 × 1 0 − 6 4 π × 1 0 − 7 × 62 × 1 0 − 6 × 4 2 = 4.88 4 π × 62 × 4 2 × 1 0 − 6 1 0 − 7 × 1 0 − 6 = 4.88 4 π × 62 × 4 2 × 1 0 − 6 1 0 − 7 × 1 0 − 6 = 1.22 π × 62 × 4 × 4 × 1 0 − 7 = 1.22 992 π × 1 0 − 4 × 1 0 − 3 = 1.22 992 π × 10000 1 × 1 0 − 3 = 12200 992 π × 1 0 − 3 = 0.255 × 1 0 − 3 m = 0.26 mm (Center pole gap)
トランス設計(構造設計) 続いて 絶縁型フライバックコンバータ回路設計:トランス設計(構造設計)-その1 | 電源設計の技術情報サイトのTechWeb
にそって進める。
設計値の整理
一次側巻線数 N p = 4 t u r n s N_p = 4 ~\mathrm{turns} N p = 4 turns 二次側巻線数 N s = 16 t u r n s , 16 t u r n s N_s = 16 ~\mathrm{turns}, 16 ~\mathrm{turns} N s = 16 turns , 16 turns VCC巻線数 N d = 10 t u r n s N_d = 10 ~\mathrm{turns} N d = 10 turns トランスコア PC44PQ20/16 ギャップ長 ℓ g = 0.26 m m \ell_g = 0.26 ~\mathrm{mm} ℓ g = 0.26 mm ギャップ長 ℓ g = 0.13 m m \ell_g = 0.13 ~\mathrm{mm} ℓ g = 0.13 mm ボビンの選定 コアと同じく特に気にせずにCPV-PQ20/16 を使うことにする。
有効巻枠の確認 巻き幅 7.82mm 巻き高さ (17.22mm - 10.80mm) / 2 = 3.21mm 巻線構成決定 「シンプルな構成」を選ぶ。
沿面距離とバリアテープ 5V, 15V, 10Vと電圧が低いので省略する。
続いて 絶縁型フライバックコンバータ回路設計:トランス設計(構造設計)-その2 | 電源設計の技術情報サイトのTechWeb
にそって進める。
線材の選定 計算せず適当に
一次側 N p N_p N p 二次側 N s N_s N s VCC N d N_d N d と決める。
結線図、層構成、巻線仕様 適当に内側から
トランス仕様決定 Coil Turns Wire Np 4 2UEW 0.26 × 7 Ns1 16 2UEW 0.32 Ns2 16 2UEW 0.32 Nd 10 2UEW 0.32
トランス製作
トランスコアとボビン 組んでみる 2D=16.2mmだから8.10mm(実測値) コアにポリイミドテープ1枚貼って8.25mm フェライトコアにポリイミドテープ1枚貼って8.25mm - 8.10mm = 0.15mm (スペーサーギャップ)
巻き線を始める 巻き線終わり テープでコアを固定 ピンにはんだ付け 完成 ブレッドボードに回路を作る
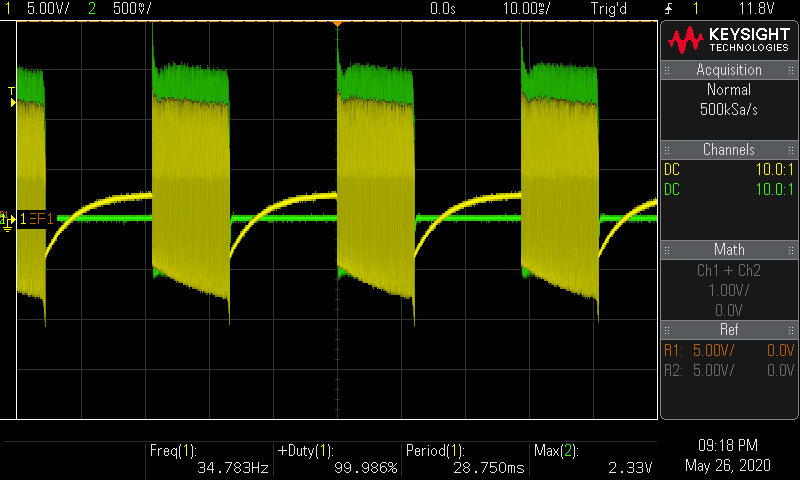
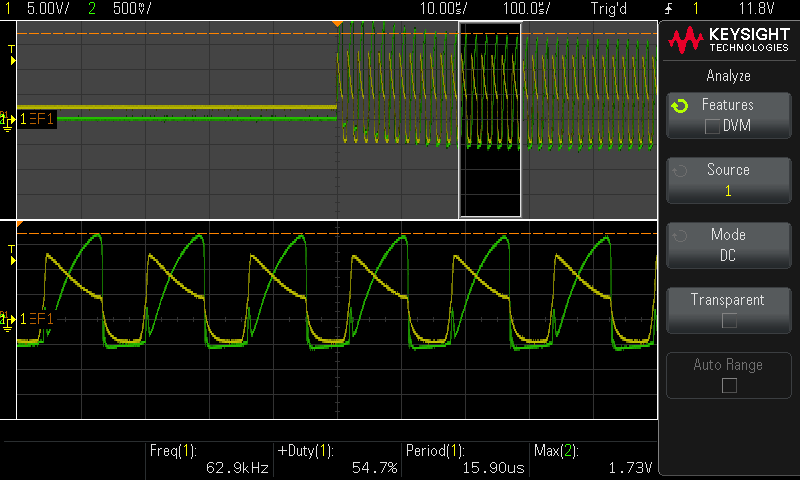
ブレッドボード上の実験回路
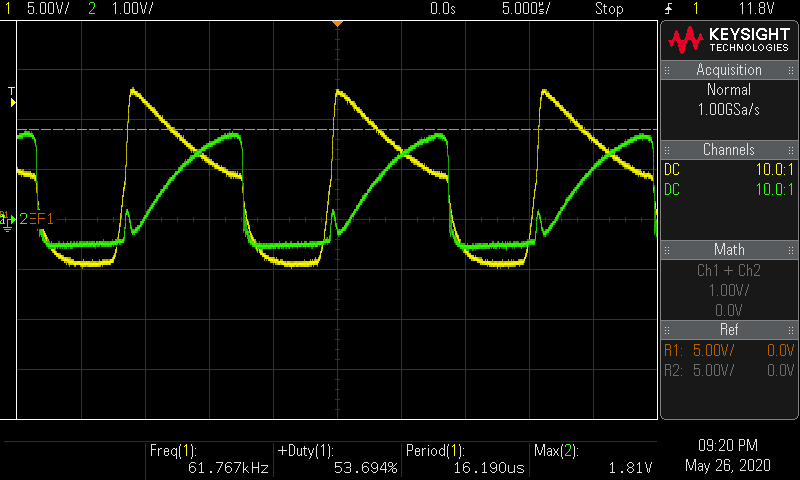
ブレッドボード上の実験回路 回路に電源(5V)を接続する ch1(黄色): MOSFETのゲート電圧 ch2(緑色): 40 m Ω 40 ~\mathrm{m \Omega} 40 mΩ
scope
scope
scope 自励型DCDCコンバータの発振周波数は61.767kHz, 二次側に正負15V出力を確認した。
40 m Ω 40 ~\mathrm{m \Omega} 40 mΩ 1.81 V 1.81 ~\mathrm{V} 1.81 V I I I
I = V R = 1810 m V 40 m Ω = 45.25 A
\begin{aligned}
I &= \frac{V}{R} \\
&= \frac{1810 ~\mathrm{mV}}{40 ~\mathrm{m\Omega}} \\
&= 45.25 ~\mathrm{A}
\end{aligned}
I = R V = 40 mΩ 1810 mV = 45.25 A
ピーク電流だけどなかなか流れているな。
出典: 「Mn-Zn系フェライト材質特性」 データーシート
出典: 「Mn-Zn系 スイッチング電源用フェライトコア PQシリーズ」データーシート
出典: CPV-PQ20/16-1S-14P-Z Drawing